Algebraic Water Flux Framework
The ’Algebraic Water Flux Framework’ comprises straightforward equations designed for easy assessments of membrane characteristics and filtration processes. Particularly, it introduces the ’filtration efficiency’ as a measure for how much the filtration process is affected by concentration polarization. I.e. rather than directly quantifying , it quantifies its resultant effect on the process as a whole. Specifically, this framework enables the quantification of a filtration process based solely on bulk variables. Moreover, it relies on dimensionless process variables, offering the advantage of generalizing filtration processes. At the heart of the framework is the algebraic water flux equation, eliminating the need for iterative solutions to determine the interdependence of water flux and concentration polarization. Details are found in Tiraferri et al. 2023.
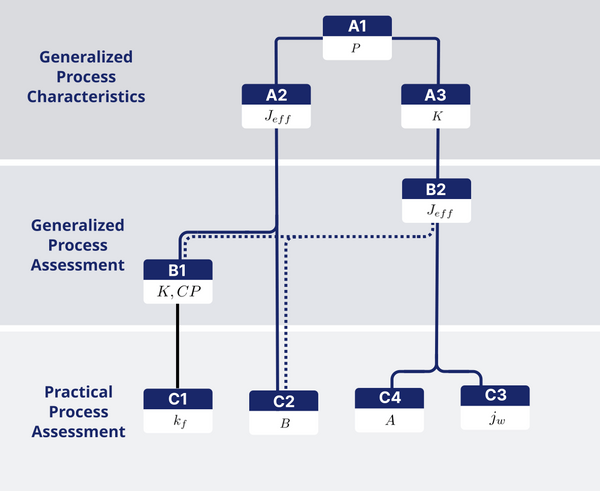
How it works: The framework consists of 9 calculators, which are grouped in sections A,B and C. Section A introduces the generalized, characteristic process variables. Section B demonstrates how the filtration process equations apply in estimating the filtration efficiency, the extent of concentration polarization and the feed solute mixing. Lastly, in C, the practical process variables , , and can be calculated from the characteristic process variables, streamlining the evaluation of membranes and/or system performance.
The framework’s calculators are indicated in the workflow diagram below. If you, for example, want to evaluate the mass-transfer coefficient in the feed channel , you would use calculator C1. The pipeline indicates that you’ll will have to use calculators B1, A2 and A1 before. The sections below will guide you through the framework.
A. Generalized Process Characteristics
The filtration process can be generalized in terms of the three characteristic dimensionless process variables. Here you can define two characteristic process variables in terms of your physical process variables. Start with defining the Pressure Modulus in A1 below. Afterwards you can chose to also define the Filtration Efficiency in A2 or the Feed Mixing Coefficient in A3.
A1 Pressure Modulus
The pressure modulus relates the applied hydraulic feed pressure with the osmotic pressure in feed and permeate, and the permeate osmotic pressure, through the rejection coefficient.
If you know the water flux , you can go to section A2 below and define the filtration efficiency (left-hand branch in figure above). With and known, you can run the Generalized Process Analysis in section B1 and proceed to section C1 to directly calculate the resultant mass transfer coefficient . Or you could directly calculate the solute permeability coefficient in C2, without B2.
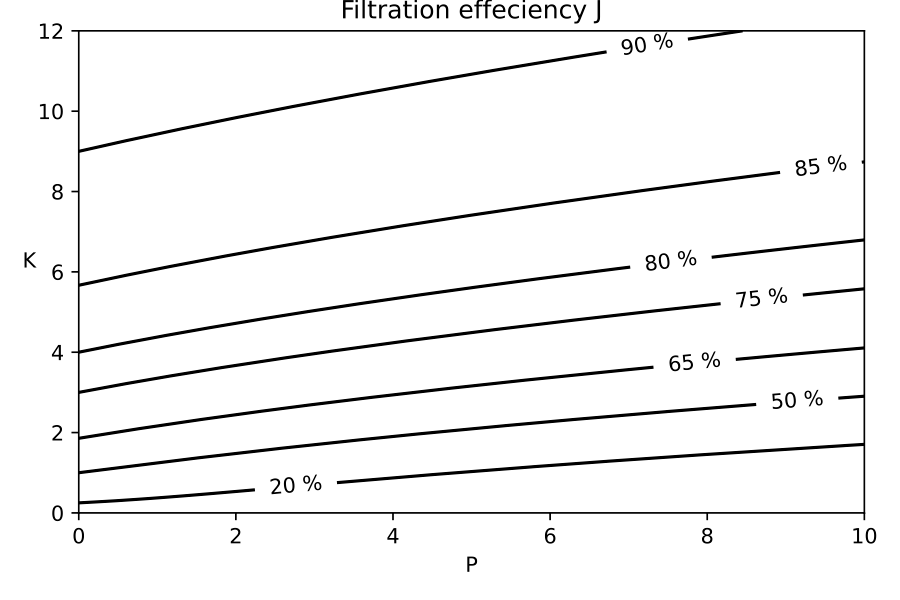
On the other hand, if you know the mass-transfer coefficient , you can go to section A3 below and define the Feed Mixing Coefficient (right-hand branch in figure above). With and known, you can then evaluate the Generalized Process Analysis through section B2. Thereafter, you can calculate the absolute water flux in section C3.
If you know both your water flux and the feed channel mass transfer coefficient , you can directly go to C4 and calculate your water permeability coefficient .
A2 Filtration Efficiency
The filtration efficiency is a measure of how much a filtration process is affected by concentration polarization. is defined as the ratio of the real water flux and the hypothetical, ideal water flux without concentration polarization .
Example: If your process yields a Filtration Efficiency of 73%, it implies that concentration polarization reduces the water flux by 27%.
A3 Feed Mixing Coefficient
The Feed Mixing Coefficient quantifies the magnitude of solute mixing in the feed channel. It is defined as the ratio of the mass-transfer coefficient and the osmotic water transport .
B. Generalized Process Analysis
You can analyze your process efficiency in terms of the characteristic variables alone. After you have defined two characteristic variables in section A, you can evaluate the remaining one here and see your process efficiency in the two figures below.
B1 Concentration Polarization & Feed Solute Mixing
The Concentration Polarization Modulus is the relative increase of solute concentration at the membrane. It is calculated here with the bulk variables and . Similarly, the Feed Mixing Coefficient is also calculated from and . It may used to calculate the mass transport coefficient in C1.
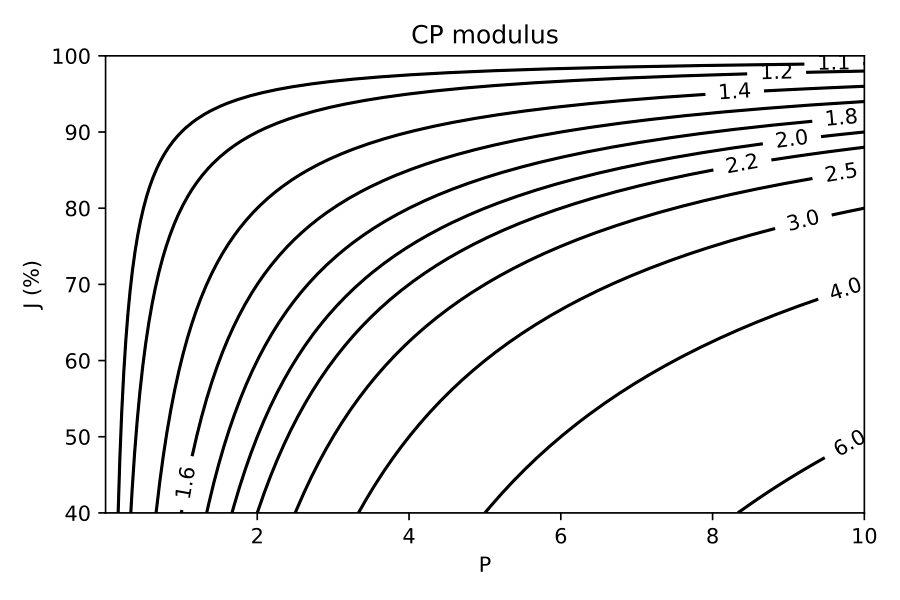
B2 Filtration Efficiency
When the water flux is unknown, the filtration efficiency is calculated using the ’algebraic water flux’ equation below. The resultant water flux can thereafter be calculated in C3. Note that this equation is a highly accurate approximation to the traditional water flux equation, provided that 4P < K(1 + K)2, see here for details.